Is Public Transit a "Public Good"? Issues with Charging Users of Different Types of Goods and Services to Use Them

There is a difference between how economists define the term vs. how other people (such as politicians) define it.

Photo Source: Calgary Transit.

Introduction

Most goods and services in an economy are allocated in markets, which is why we tend to concentrate on them when studying Economics. Even so, there are things one can obtain without paying anything, which creates a special challenge for us because:

• Market forces that normally allocate resources in our economy are absent. In Principles of Microeconomics courses, we learn free competitive markets will allocate goods to consumers that need them most as they are willing and able to pay the most for them. Similarly, the most efficient suppliers will sell goods in these markets as they are willing and able to charge the lowest prices for them. However, if people can obtain it for nothing, then this price mechanism is absent.

• Private markets cannot ensure that the goods and services are produced and consumed in the proper amounts. If the price mechanism is absent, then there is no way for the free market to efficiently allocate resources (a market failure).

In such cases, government policy can potentially correct this market failure, thus raising economic welfare (total surplus). With that in mind, this issue of Ride On will proceed as follows:

1. We will introduce four types of goods — pure private good, natural monopoly, pure public good and common resource — and identify sources of market failure.

2. Next, we will examine how to find the social optimum for each of these goods.

3. Third, we will explore the feasibility of regulating a natural monopoly in order to move closer to the social optimum, and ask whether regulation is even necessary.

4. We will then learn why public goods and common resources are unlikely to be produced without government intervention.

5. Finally, we will see how buyers can be “tricked” into revealing true preferences.

But before we begin, if you enjoy what we write and find it valuable, please consider a paid subscription. It will help us to devote more resources into what we write so it will get even better! Also note our 2-for-1 sale on annual Substack subscriptions remains in effect until March 31, and you can learn more about it here.

Thank you for coming along on this ride with us!

Four Types of Goods and Services

While many people — such as politicians — call anything provided by the government a “public good”, that is not how economists define them. In our definitions, we group goods and services based on two characteristics:

1. Excludability: assuming no government intervention at all, can we stop someone from using the good or service if they do not pay for it?

2. Rivalry: assuming no government action, does one consumer’s use of the good or service preclude someone else’s use of it (either simultaneously or over time)?¹

Based on these characteristics, we can divide goods and services into four categories:

1. Pure private goods: these goods and services are both excludable and rival; they are the ones we typically assume in economic analyses. For example, if I want to obtain coffee I must pay for it; once I drink it, no one else can drink it.

2. Natural monopolies (non-congestible private goods): they are excludable but not rival, so everyone can use them but they must pay for them first. For example, Telus can exclude me from using its long-distance phone services if I do not pay for them, but anyone can use them simultaneously if they also pay for them.

3. Pure public goods: they are both non-excludable and non-rival. For example, national defence is non-excludable because the government cannot say “you did not pay for it, so we will only let the bombs hit you!” It is non-rival since keeping some Canadians safe from attacks does not leave other Canadians vulnerable. We all benefit from security provided by the Canadian Armed Forces. In fact, that is an argument in favour of more funding for national defence: our Armed Forces are doing what they can to protect us, but they are capacity constrained.

4. Common resources (congestible public goods): they are non-excludable but rival. For example, fish in the ocean are non-excludable since the government cannot effectively stop people from fishing along such a long coastline; they are rival because the fish I catch (and keep) cannot be caught by anyone else.

Therefore, in the case of pure private goods and natural monopolies, market failures arise due to excludability (market power). On the other hand, market failures arise with common resources and pure public goods due to non-excludability (missing markets).

Note it is difficult — if not impossible — to find a good or service which is perfectly rival or perfectly excludable, so the above four types of goods and services do not literally exist. Instead, think of “rivalry” and “non-rivalry” as being endpoints on a continuum where one good is more rivalrous than another; think of “excludability” and “non-excludability” similarly.

With that in mind, we need to carefully consider the context in which we are examining the good or service in question. For example:

• Public transit is technically excludable regardless of the mode of transportation — for example, trains, buses, etc. — because someone can be denied access if they do not pay. However, trains are likely less excludable than buses because while we must pass a driver to ride the bus, Calgary Transit does not have the resources to check every single train passenger for proof of payment.

• With respect to rivalry, national defence is a common example of a pure public good. However, the benefits of a distant early warning system are likely less rival than soldiers patrolling an area because once a missile is detected, it is detected for everyone; on the other hand, soldiers cannot patrol everywhere at once.

Therefore:

• To determine the level of excludability, think of the costs of exclusion (time, money and other resources): the more costly it is to exclude someone from using the good or service, the less it is excludable.

• To determine the level of rivalry, think in terms of supply and demand: if there is an excess supply of the good or service in normal circumstances, then it is non-rival; if there is no excess supply in normal circumstances, then it is rivalrous.

To summarize the differences between each type of good, see Figure 1 below which uses a quadrant system. We have also provided examples in each quadrant.

Figure 1: Four Types of Goods with Examples

To use transport-related examples, congested toll roads are pure private goods to economists because anyone who does not pay the toll can effectively be excluded from using the road, while the congestion makes using these roads rivalrous. But if these toll roads are not congested, then rivalry is not much of an issue, so they are natural monopolies (also known as toll goods).

But if they are non-toll roads, then they are not excludable. Therefore, congested non-toll roads are common resources, while uncongested ones are pure public goods.²

Notice education and healthcare are considered by economists to be pure private goods, even if they are publicly provided. That is because it is possible to exclude people from using those services if there are fees to using them — as shown in the U.S. healthcare system, as well as with private schools.

They are also rivalrous since class sizes are capacity-constrained, as is healthcare — as anyone who has spent many hours in a Canadian hospital waiting room can attest.

Finding the Social Optimum for Private and Public Goods

Due to the non-rivalrous nature of public goods and common resources, their demand curves are derived differently than for a private good or natural monopoly. However, the supply curve is generally derived the same for all of them because all suppliers want to make money; the problem is just getting people to pay for what they have!

For this example, we are classifying public transit as a private good because we are assuming it is rush hour, so buses are crowded enough to make riding rivalrous. And we also focus on buses — not trains — so riding is much more easily excludable.

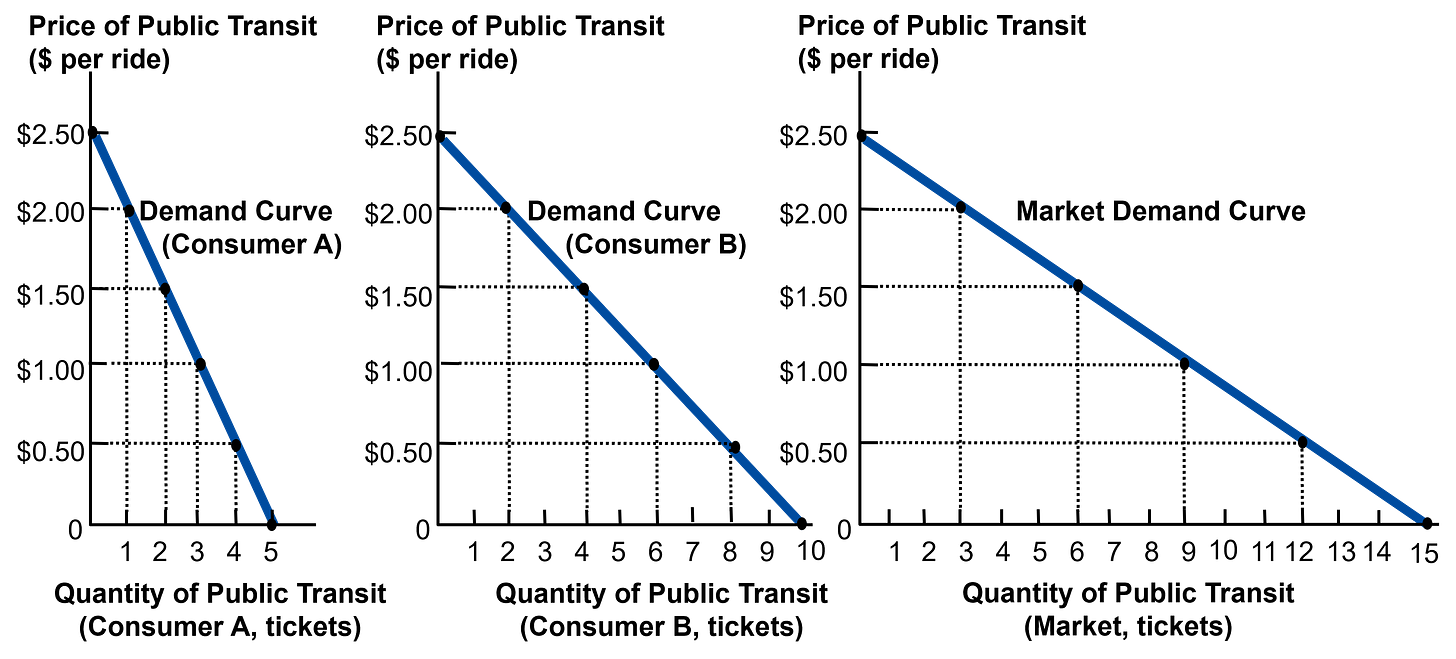
The derivation of the market demand curve for a private good should be familiar from a Principles of Microeconomics course, but for fun we will derive it again in Figure 1.

There are two consumers in the market for public transit: Consumer A and Consumer B. Consumer A’s demand ranges from five tickets when they are free, to zero tickets when the price is $2.50 per ticket. Consumer B’s demand curve is similarly derived, except we assume they are willing and able to purchase twice as many tickets as Consumer A at every price level.

Figure 1: Deriving Social Optimum for Private Good

To find the market demand curve, we sum each consumer’s quantity demand at every price, which is also known as summing the quantities demanded horizontally. Thus, if the price of tickets is zero then the quantity demanded for the entire market is 15 tickets: five tickets for Consumer A plus ten tickets for Consumer B. If the price of tickets rises to 50 cents per ticket, then the quantity demanded by the market is 12 tickets: four tickets for Consumer A plus eight tickets for Consumer B.

We can continue to calculate each market-level quantity demand for all other prices, and then join the points that result to draw the market demand curve in Figure 1. The equilibrium price and quantity are then found simply by finding the intersection of the market demand and supply curves (not shown above).

Now suppose we instead look at a public good where we cannot exclude someone from using it (Figure 2). We could use the case of an uncongested non-toll road, but for fun we will instead use national defence as an example.

We again assume two “consumers” and each one has its own individual demand curve for this service. This time, the service is non-rivalrous so if one person consumes G* units of defence, then so does everyone else. As such, we find the market demand at quantity G* by summing the amount each person is willing to pay for that amount of defence — i.e., we sum vertically. We would do the same for every possible amount of defence to get the top (red) line in Figure 2.

Figure 2: Deriving the Social Optimum for a Public Good

As with a private good, the equilibrium price and quantity is then found where the market (aggregate) demand and supply curves intersect.

Question: Under what conditions is total surplus maximized when we are dealing with a public good?

As with a private good, we set the price of a public good such that marginal benefit (MB) equals marginal cost (MC) — same reasons as a private good where we call it “revenue” instead of “benefit” — where each point on the supply curve represents MC.

But to be more specific, given the way we derive the demand curve for a public good, we want to set:

∑_i MB_i = MC.

where i represents an individual consumer, so if there are three consumers then we would set:

MB₁ + MB₂ + MB₃ = MC

Regulation of a Natural Monopolist

Now that we know how to derive the demand curves, and thus the social optimum for each type of good and service, let’s now think about how we can regulate a natural monopoly so we can try to achieve the social optimum.

There are various methods of regulating a natural monopoly, two of which are:

1. Open access rules: under these rules, the natural monopolist is required to share its resources and infrastructures with new entrants for a fee. For example, prior to the 1990s the incumbent long-distance carriers across Canada — for example, Telus in Alberta and Bell Canada in Ontario — had natural monopolies because the fixed costs of creating a competing long-distance carrier were too high to justify entry. Thus, in the 1990s the federal government created open access rules which required Bell Canada and Telus to grant new entrants access to their infrastructures, as long as the new entrants paid for such access. As we have seen over the years, these rules have led to much lower prices and better service — although there are still legitimate complaints against these companies.

2. Cost-based pricing: recall from any Principles of Microeconomics course that the most efficient equilibrium is where firms set their price equal to marginal cost, because then they are making no profits at the margin. Therefore, it might seem sensible for the government to require the natural monopolist to set P = MC, known as marginal-cost pricing. However, this regulation might be infeasible in practice as shown in Figure 3 below.

Figure 3: Cost-Based Pricing

In this figure, we see that in a free market the natural monopolist will set its quantity where MR = MC, so its price will be P_M > ATC and there is a deadweight loss (DWL) covering Area ABDCE — the red and orange triangles — where the DWL is defined as the loss in economic welfare due to the firm pricing too high, and selling too little, relative to the social optimum at Point C.³

To eliminate this DWL entirely, a government could require the monopolist to set its P = MC so it sells Q_C at a price of P_C. This sounds all well and good as it eliminates the DWL and thus maximizes total surplus, but it also requires the monopolist to price below its average total costs. Clearly, the government cannot force a business to price so low as that firm would rather shut down than to lose money in the long term.

A potential second-best solution is to require average-cost pricing: the monopolist prices just high enough to cover its average total costs, so it sets its price equal to P_AC and sells Q_AC units of its good. There would still be a DWL triangle covering Area CDE — the orange triangle — but that triangle is much smaller than Area ABDCE. In short, the government regulation has led to welfare gains.

What are some practical problems with implementing average-cost pricing? It requires the government to accurately estimate the firm’s average cost curve, which is very difficult. That is why central planning typically does not work: the government does not understand the day-to-day operations of every business — nor can it — so it cannot effectively determine what is optimal to the entire economy.

Is regulation of a natural monopoly always necessary? Not if the market is contestable, which means barriers to entry and exit are so low the monopolist needs to price at (or near) the competitive level to prevent entry.

There have been economists who argued the airline industry is contestable because they viewed entry and exit to be very easy. However, we have our educated doubts this is true because they are large sunk costs to enter the industry.

Even if we argue competing airlines can just move aircraft and employees between routes when profitability possibilities arise, it would be too costly to do so often — not just in monetary terms but also in terms of maintaining consumer loyalty, as consumers want to know their tickets will be honoured when they want to use them.

Free Rider Problem and Tragedy of the Commons

We will now demonstrate why it might be necessary for a government to intervene in a market where there is a pure public good or common resource.

It might not be feasible for a provider of these goods to exclude people from enjoying their benefits because — assuming no credible social punishment mechanism such as guilt or shame — people will just wait for other people to pay for it instead, and then still use it themselves.

Photo Source: The New York Times.

We call this problem a free-rider problem, where a free-rider is a person who receives the benefit of a good but avoids paying for it, either with money or time. The free-rider problem prevents private markets from supplying non-excludable goods, which is why we sometimes call it a missing-market problem. To solve this problem, the government can decide to fund the provision of a public good with tax revenues — after conducting a cost-benefit analysis, of course.

A related problem is known as the Tragedy of the Commons: a parable that illustrates people will overuse common resources — such as fish in the ocean — to maximize their own welfare, but they hurt society since they ignore the negative effects of overconsumption on others. An example of this tragedy occurred in the 1990s when Spanish fishermen were accused of overfishing off the coast of Newfoundland.

We will use game theory to demonstrate this problem. The game is summarized as follows, and shown in Figure 4 below:

1. Players: Fisher 1 and Fisher 2

2. Rules:

   1. Each can choose to either Fish Lots (F) or Restrict Fishing (R)

   2. They (essentially) make their choices simultaneously

   3. Each player has complete, perfect, and symmetric information

3. Outcomes: (F, F), (F, R), (R, F), (R, R)

4. Payoffs: if both players fish lots, then they will each make a payoff of 2. However, if one fishes lots and the other restricts their fishing, then the over-fisher will raise their payoff to 4 by catching fish the other player is no longer catching, while the one restricting their fishing will reduce their payoff to 1. But if they both restrict their fishing, then they will each make a payoff of 3 — which is higher than if they both fish lots because they are conserving the fish stock, so they can make more money over time.

Figure 4: Tragedy of the Commons

To solve this game, we begin by assuming we are one of the two players. It does not matter which player we choose first, so suppose we are Fisher 2 and we assume Fisher 1 fishes lots. In that case, Fisher 2 has a choice of fishing lots and making a payoff of 2, or restricting their fishing and earning a payoff of 1. Clearly, Fisher 2 is rational so they want to fish lots. We then circle their payoff of π₂ = 2 to represent a best response.

To properly solve the game, we must exhaust all possible moves that could be made by Fisher 1. We already figured out Fisher 2’s best response to Fisher 1 fishing lots, so we must now determine his best response if Fisher 1 restricts their fishing. In that case, Fisher 2 can either fish lots and earn a payoff of 4 or restrict fishing an earn a payoff of 3. Since Prisoner 2 is rational, he will choose to fish lots and minimize his prison sentence. Thus, we circle π₂ = 4 to represent another best response.

We can now see that Fisher 2 has a strictly dominant strategy: fish lots. Since they will never choose to restrict fishing, we can safely ignore that strategy. Given complete, perfect and symmetric information, Fisher 1 understands this strictly dominant strategy and will thus only have to decide whether or not to fish lots given Fisher 2’s obvious preference for fishing lots: if Fisher 1 also fishes lots, they will earn a payoff of 2 instead of 1 if they restrict their fishing. Being rational, they will obviously choose to fish lots so we circle π₁ = 2 to represent a best response.

We have now exhausted all possible strategies, and we see there is only one cell in the table where both payoffs are circled — and highlighted in yellow — as best responses: (F, F). That cell is the unique solution of the game, as neither player can unilaterally improve their payoff by changing their strategy if they finds themself in this cell.

However, if they could enforce a binding agreement with one another to make this a cooperative game, then the fishers would choose to restrict fishing. Doing so would result in both players earning payoffs of 3, i.e., the payoffs circled in red. The problem with reaching this jointly-optimal strategy lies in their inability to enforce the cooperative agreement, thus making it a Prisoner’s Dilemma: both players would be better off if they cooperated and chose different strategies, but neither one can trust the other to keep their end of the bargain due to the rules of the game!

Revealed Preference Methods

So far, we have shown that to obtain the efficient price and quantity of a public good, we need to determine each consumer’s marginal benefit of it. A question naturally arising from this statement is: how do we determine these marginal benefits?

Lindahl Solution

One potential method is known as the Lindahl Solution: each consumer honestly reports their marginal benefit and then pays their “fair share” based on it. This solution can exist for private goods in competitive markets, because a consumer who lies will reduce their equilibrium quantity purchased, thus reducing their total benefit of consumption.

However, due to the free-rider problem one cannot simply ask consumers to report their marginal benefits for a public good or common resource, since they will have an incentive to lie; assuming enough other people are honest, that consumer can say they want only want a small quantity, but they will not be bound to this lower quantity because the good or service is non-excludable.

Alas, everyone will likely think the same way so everyone will underreport their true preferences, leading to a situation where no one is satisfied.

In short, these consumers find themselves in a Prisoner’s Dilemma: they all prefer everyone is honest, but each individual has a dominant strategy to be dishonest due to the free-rider problem. Thus, we need to figure out how governments can “trick” them into revealing their true preferences.

User Fees

If MC = 0 for public good, then we set P = 0 to get the efficient solution. A problem with this approach is there can be large fixed and sunk costs of providing the good, and they are not included in MC — because “marginal” essentially means “change in”, and fixed/sunk costs do not change with quantity.

A potential solution is to charge a fixed user fee to use the good — small enough to cover fixed costs while excluding as few consumers as possible.

User fees can include:

1. Indirect user fees: for example, gasoline taxes to fund highway construction, which are avoidable by not buying a car. In a public good context, we assume it is too expensive to exclude people from the highway. In fact, gasoline taxes are levied in Vancouver, Victoria, and Montreal for the specific purpose of funding public transit.

2. Subsidies and partial user fees: for example, education and healthcare, such as ambulance services which are publicly-funded but users still have to pay for use. Alternatively, think about the LRT where the provider can charge user fees (fare) small enough to make the opportunity cost of not paying too high, and governments subsidize the rest.

3. Non-linear pricing: for example, pay a fee to get onto a toll road and then pay additional fees for every kilometre driven, or pay for a transponder and then pay more for each time you use it. Alternatively, charge different rates at different times of day, or offer quantity discounts. In a public good context, a private firm might not be able to effectively exclude people from the highway, but the government can spread the cost of enforcement across a wider population via taxes and use those resources to enforce the tolls.

Graphically, see Figure 5 below, where we have drawn the average total cost curve which just averages the fixed cost of providing the good or service over the number of users — we assume no variable costs. Since the user fee is the price in this case, it will fall as the number of users increases.

Figure 5: User Fees

We can see that any point on the AC curve is self-financing, and the more users we have, the lower the user fee needs to be. But at the second equilibrium, (n – n₂) potential users are excluded from the market, so this equilibrium is inefficient.

Also, if the population is less than n₁ — a very small community — then average costs are higher than demand so we cannot charge them a user fee to provide the good, even though it does cover MC and thus passes the cost-benefit criterion.

What are some “pros” of user fees?

• Indirect user fees can be more attractive politically than direct user fees, because they are easier to hide from voters.

• They allows the provider to cover costs for the public good more easily than other methods — such as asking them to pay what they are willing to pay.

• Contrary to taxes, people are not forced to pay for what they do not buy — so they are more efficient than taxes.

• Accountability is increased because on the sides of producers, if consumers are charged directly for product — as opposed to it being paid out of tax revenues — then they will demand good quality; on the side of consumers, charging a direct user fee might encourage them to not overuse a common resource, or to overuse a service provided using tax revenues.

What about “cons” of user fees? The main concern is related to social justice: despite the efficiency benefits of user fees, they can hit poorer people a lot harder than higher-income people — for example, prescription refill fees can be regressive.

Tiebout Locational Choice Mechanism

According to Tiebout, people will move to where the price (tax burden) of public goods most closely resembles their marginal benefit of using these goods.

Therefore, if someone wants a big social safety net, and they are willing to pay for it through taxes, then they will move to such a jurisdiction. But if they are more laissez-faire philosophically, they will move to that kind of jurisdiction.

This is not a perfect solution in terms of efficiency — compared to the Lindahl one where there is only one jurisdiction in which everyone pays their marginal benefit — but it is closer to the Lindahl solution than if we had only one jurisdiction and no way to determine marginal benefit.

What are some problems with this mechanism?

• It assumes no costs of moving, such as monetary costs, emotional attachments to family, language barriers, immigration/emigration barriers, etc.

• People might move to areas with low taxes because they do not like taxes and do not care about services. That is good. But some unemployed people might stay in a jurisdiction with no job, rather than move to where a job exists, because the welfare system in their home jurisdiction is so relatively generous. Thus, welfare benefits in the home jurisdiction outweigh job benefits in new jurisdiction.

• Race to the bottom: suppose we have a high-tax/high social benefit province, as well as a low-tax/low benefit province. People in the first province who are relatively more able to pay taxes might move to other jurisdiction to avoid taxes; that leaves the first jurisdiction with no one able to pay the taxes, so those left cannot get services they want. This can be made even worse if the government in the first jurisdiction lowers taxes/services to keep productive people from leaving, so the provinces are engaged in one some call a “race to the bottom”.

Closing Remarks

All of this talk about wanting something but we don’t want to pay for it puts the classic band Jane’s Addiction into our heads! So let’s watch that video now.

Thank you for reading to the end. If you like what you see and want to support us with a paid subscription, then slam the “subscribe” button below! Regardless, we are glad you are here. We hope you have a weekend!

1. Notice we are focusing on rivalry between consumers, not between producers in this context.

2. You might be wondering why economists consider non-toll roads to be non-excludable, since something is only non-excludable if we cannot make people pay for it. In other words, can we not just make it a toll road? That is true in some instances — such as Highway 407 in Toronto — where there are a limited number of entrances to that highway, so it is rather easy to enforce the toll system. But with roads that are easily accessed from many different points, setting up the toll system and enforcing it would be much too cost-prohibitive.

3. Notice the curve is downward sloping, implying economies of scale: a new entrant would have to start off at a high point on this curve because they have to incur large fixed start-up costs. However, the incumbents are already at a low point on this curve because they have been able to expand their businesses, thus spreading their fixed costs over a large quantity. Therefore, new entrants cannot possibly compete with incumbents, enabling the incumbents to be natural monopolists.